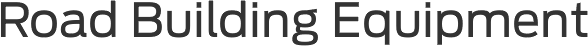Engineering rollers

In Versions 1 and 2, the roller constantly pivots on a vertex, even towards the top and bottom, additionally the length toward opposing contact point is always the exact same.

In Version 3, the width for the non-round roller at any point is defined by a straight line that works through the vertices associated with the triangle and through triangle itself. Each such straight line could be the amount of two radii—the distance of one big arc in addition to distance of just one little arc. Including, the straight-line PO in the drawing below (mouse click to enlarge) is the sum of the radii of arc HG (a large arc) and arc DE (a tiny arc).

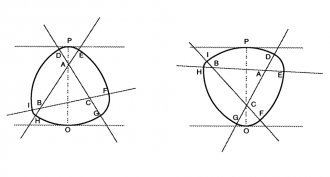
Assume you have got a roller such as the one shown within the diagram overhead. Let’s say the roller is resting on point O. As roller moves on arc HG, with its resting point approaching H, the board over the roller will be rolling on arc DE. The board will remain amount because roller’s width (which is the amount of the distance of arc DE in addition to distance of arc HG) will likely to be constant.

Suppose the roller rolls until it rests on point H. Its width is still the sum of the two radii—the distance of arc HI plus the distance of arc EF. Because arc HI and arc HG have point H in accordance, and because arc DE and arc EF have point E in keeping, the width associated with the roller must still be continual. Due to the fact roller goes on rolling and reaches point I, similar debate pertains, additionally the width associated with roller is almost always the exact same.

Once you attempted to pick a center for the non-round roller, you could logically have plumped for the triangle’s centroid. Another rational choice will be the point halfway between your top and bottom regarding the roller for a certain direction. Neither of the things, however, remains at a consistent level due to the fact roller rolls. As an alternative, they explain an up-and-down movement. While you noticed, no point on the roller remains a consistent height since the roller moves. As a result, the rollers will make lousy vehicle wheels. (Where can you place the axle?)